Know Your Support Vectors(Support Vector Machine)
Support Vector Machines
It is a two-part article wherein first part I will discuss about the hard-margin SVMs and in the next part I will discuss about soft-margins and kernels.
A Support Vector Machine (SVM) is a very powerful and versatile Machine Learning model, capable of performing linear or non-linear classification, regression, and even outlier detection and anyone interested in Machine Learning should have it in their toolbox.
What is the need of SVMs when we have Logistic Regression?
In my previous article about Logistic Regression(check the link)we have discussed how it helps to solve the classification problems by separating the classes with the help of hyperplane, but there can be infinite number of hyperplanes and logistic regression chooses arbitrarily any one of them. This problem will be more clear by seeing the below image.
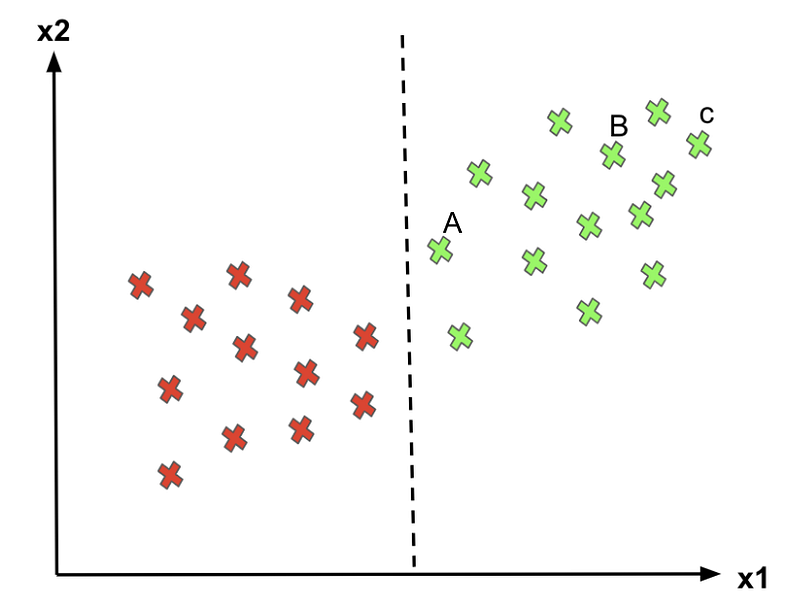
Our focus point should be C and A, for C it classifies as 1 very clearly because it lies far from the decision boundary but for class A even it classifies it as 1 but any change in the position of the decision boundary to the right would classify A as 0. So as the point is farther from the decision boundary we are more confident in our predictions. Therefore, the optimal decision boundary should be able to maximize the distance between the decision boundary and all instances. i.e., maximize the margins. That’s why SVMs algorithm is important!.
What is Support Vector Machines(SVMs)?
The goal of the SVM algorithm is to create the best line or decision boundary that can segregate n-dimensional space into classes so that we can easily put the new data points in the correct category in the future. It is also known as the Widest Street Approach.
SVM chooses the extreme points/vectors that help in creating the hyperplane. These extreme cases are called as support vectors, and hence algorithm is termed as Support Vector Machine. Consider the diagram below in which there are two different categories that are classified using a decision boundary or hyperplane:
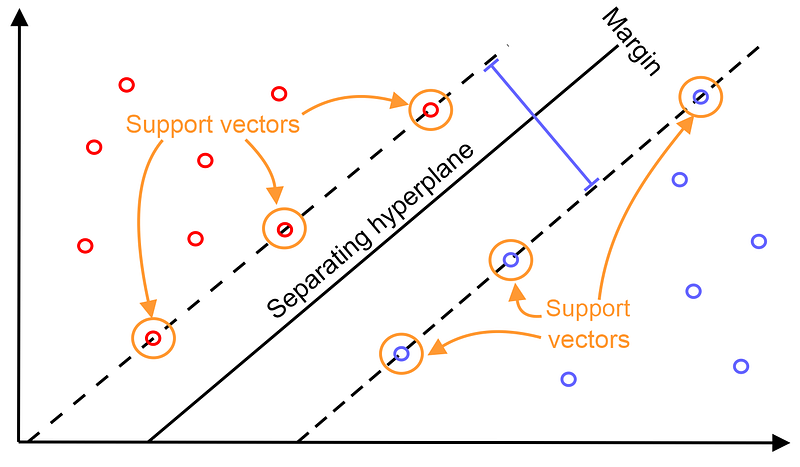
It can be seen as a street and our aim is to find the hyperplane that has the maximum margin hence the name widest street approach.
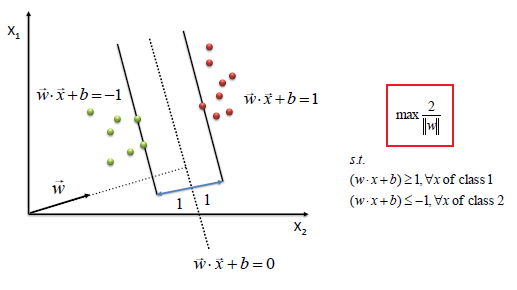
Let’s say we have some positive points(red) and some negative points(green) and the hyperplane vec(w). Now to classify a point as positive or negative we have to project that point onto the hyperplane and if (w.x+b)≥ 1 we will classify it positive else negative.Now for prediction we only need to know the sign of the predicted value i.e y_pred = sign(wx+b)if it returns +1 it’s positive and if -1, then negative.
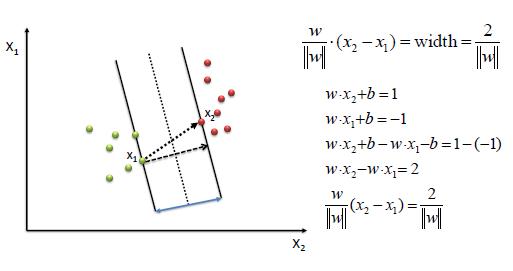
Now to find an optimal hyperplane we need to maximize the width(w). Maximizing w means we need to minimize the equation 1/2||w|| and for mathematical convenience we square the term and now we need to find w and b which minimize the equation given below.
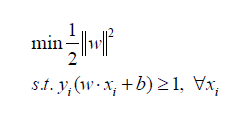
This is known as Hard Margin SVMs because in this data needs to be perfectly separable in order for SVMs to work well but what happens when the data is in the other forms like non- linear or what if the data is noisy and lot of outliers are present in the data? There arose the need of soft margin SVMs and Kernels which we will get familiar with in my see in the article.
To learn more about SVMs here are some of the useful links which helped me better understand SVMs.
Suggestions are always welcomed. Don’t forget to checkout my other articles.
Linear Regression from scratch.
Comments
Post a Comment