K-Nearest Neighbors

K-Nearest Neighbor(k-NN)

The k-nearest neighbors (K-NN) algorithm is a simple, easy to implement supervised machine learning algorithm. The “K” in k-NN refers to…

K-Nearest Neighbor(k-NN)

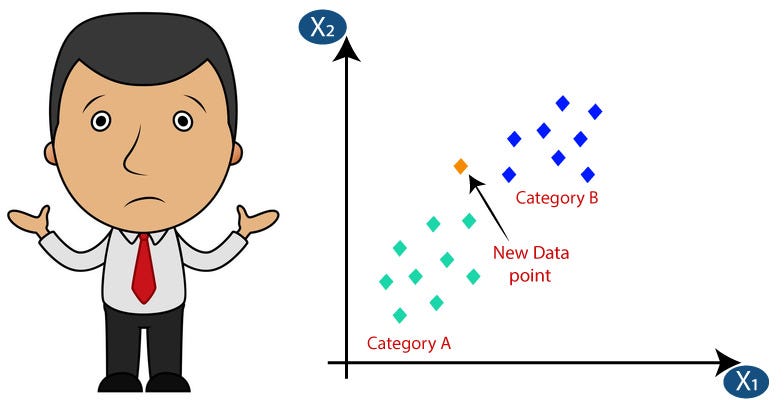
The k-nearest neighbors (K-NN) algorithm is a simple, easy to implement supervised machine learning algorithm. The “K” in k-NN refers to the number of nearest neighbors it will take into consideration while making a decision. It is commonly used as a classification algorithm but we have seen cases where k-NN is used as a regression algorithm and outperformed many of the regression algorithm.

K-NN is also termed as lazy learner because it doesn’t learn anything from the training data instead memorizes the whole training dataset and at the time of classification, it performs an action on the dataset.

The K-NN algorithm itself is fairly straightforward and can be summarized in the following steps:

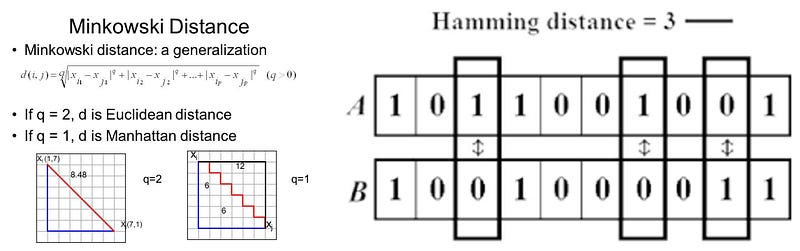
1. Choose the number of k and a distance metric. Distance metric can be Euclidean, Manhattan, Hamming or Minkowski Distance.

2. Find the k nearest neighbors of the sample that we want to classify.

3. Assign the class label by majority vote.

Based on the chosen distance metric, the k-NN algorithm finds the k samples in the training dataset that are closest (most similar) to the point that we want to classify. The class label of the new data point is then determined by a majority vote among its k nearest neighbors.

Let’s understand the working of k-NN with a simple example listed on the scikit-learn page.

sklearn.neighbors.KNeighborsClassifier - scikit-learn 0.22.2 documentation
Classifier implementing the k-nearest neighbors vote. Read more in the . Parameters n_neighborsint, optional (default =…scikit-learn.org

X = [[0], [1], [2], [3]] 
y = [0, 0, 1, 1] #class-labels
from sklearn.neighbors import KNeighborsClassifier #import
neigh = KNeighborsClassifier(n_neighbors=3, metric='Euclidean')#k=3
neigh.fit(X, y) #training 
print(neigh.predict([[1.1]])) #new or unknown data.
[0] #output

So we trained our k-nn model with data as 0 , 1 , 2 and 3 with class-labels or output as 0,0,1,1 respectively. Taking the value of k as 3 and distance metric as euclidean.

Now after training our model we have provided or model with a test data as 1.1 and the machine calculates the euclidean distance with all the input data and then outputs the results as 0.

Let’s see the internal working of k-NN algorithm. Euclidean Distance is given by the formula.

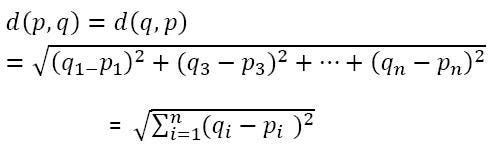
If p and q are points of interest so the euclidean distance between p and q

Now we will calculate the distance between the test data(1.1) and the training data and choose the nearest three distances.

Euclidean Distance  Class-Label

(1.1–0)² = 1.21         0

(1.1–1)² = 0.01         0

(1.1–2)² = 0.81         1

(1.1–3)² = 3.61         1

So the least 3 distance nearest to the new point 1.1 is 1.21, 0.01 and 0.81 with their class-labels as 0, 0,1,1 respectively. So, on majority basis the class-label of the new point is 0.

Advantages of k-NN

Simple
Only one hyper-parameter to tune(k)

Disadvantage of k-NN

Slow algorithm
Curse of dimensionality
Sensitive to outliers, missing data etc.

Applications

Text Mining
Agriculture
Finance

Terms Alert :

Supervised Machine Learning : Its a type of learning in which machine is provided both the input data and the class-labels and from that data machine learns the relationship between input and output and predicts the result for the unseen data. Other type of learning includes unsupervised and reinforcement learning.
Manhattan Distance : The distance between two points measured along axes at right angles. In a plane with p1 at (x1, y1) and p2 at (x2, y2), it is |x1 — x2| + |y1 — y2|.
Hamming Distance : The number of bits which differ between two binary strings. More formally, the distance between two strings A and B is ∑ | Ai — Bi |.